Augmenting RANS With Flow Transition Equations For Better Drag Prediction On 2D Airfoils

As already discussed in My previous post, ordinary RANS models such as k-w-sst seem to struggle to get reasonable drag values, especially in low to medium reynolds flows, because they are not equipped to properly predict the tranisition point from laminar to turbulent flows, which can signficantly affect the drag forces on a streamlined object such as an airfoil.

In order to decrease the severity of this issue, one can employ several augmentations to such RANS models, or use compeltely new RANS models, that attempt to predict transition in the flow.

In this project iteration, new models such as k-kl-w, and k-w-sst (gamma-algabraic or gamma-transport) were used in order to gauge how much of a positive difference they made.

All of the mesh, geometry and other related settings were the same as My previous post.

the baseline k-w-sst was kept for comparison purposed, but it should be noted that the gamma-algebraic and gamma-transport augementations were bundled on top of the baseline k-w-sst model. The k-kl-w is a seperate RANS model altogether and it has 3 transport equations rather then the 2 equations of the k-w family of RANS models, which means that it will most likely take longer to convergene (a.k.a. higher computational cost).

          Results

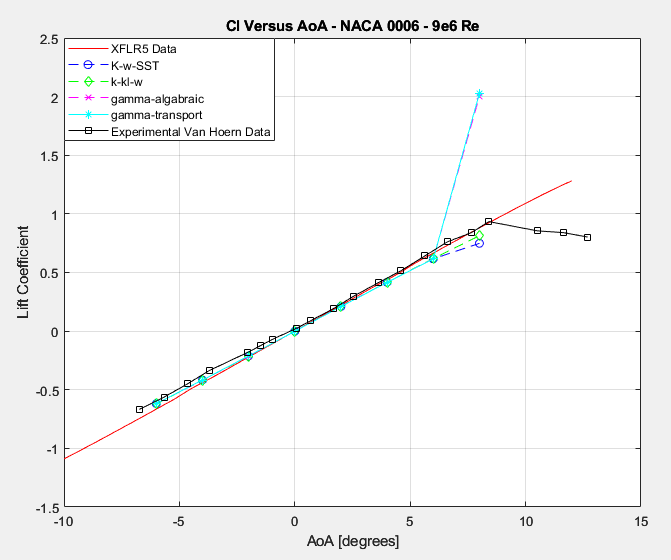
As seen in the figure above, all new models seem to predict lift values quite well, which is not unexpected since lift is generally much easier to predict accurately using numerical methods.

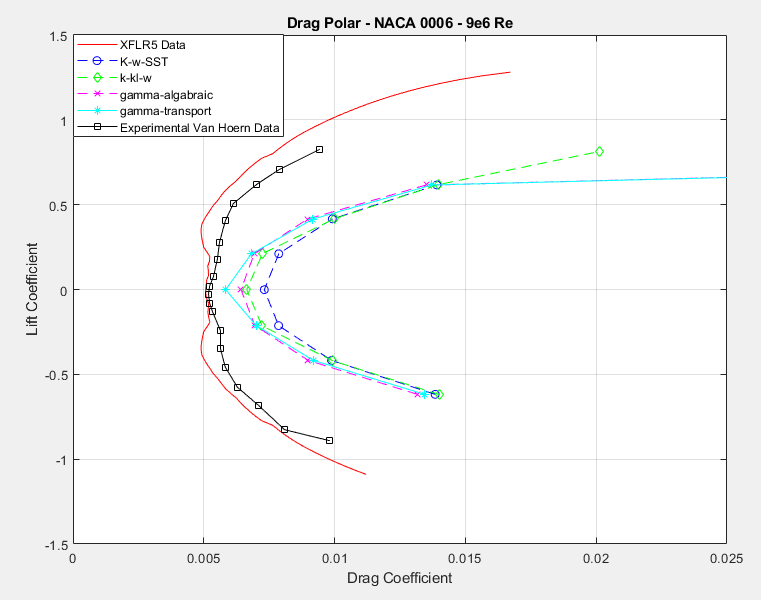
What is suprising, however, is the excellent reduction in drag by employing the gamma-transport model, which at least for low angles of attack reaches within 25% of the actual drag value. The gamma-algabraic augment is not far behind and is signficantly better than the k-w-SST base model. Despite its additional transport equation, the k-kl-w model didn't provide any additional improvement in accuracy compared to the gamma augments, which is rather dissapointing.

Unfortunately, all models still failed to provide reasonable drag values at higher angles of attack and seem to massively  overpredict drag, potentially due to premature predicition of flow seperation.

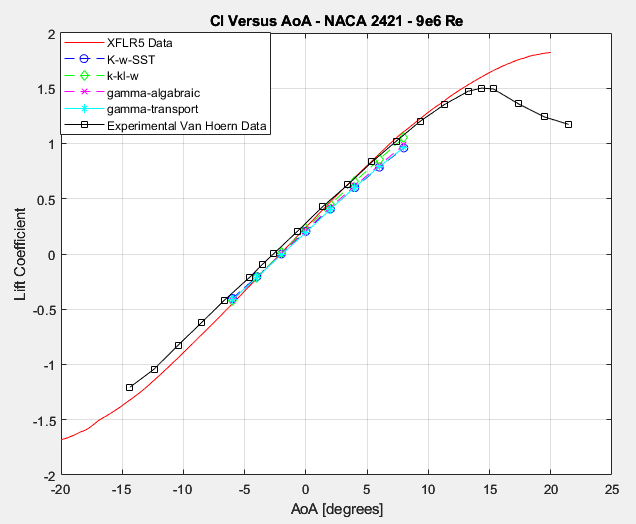
With respect to the thicker NACA 2421 airfoil, the story seems to be similar to that of the NACA 0006 airfoil. Specifically, the lift values are not particularly sensitive to the specific model being employed.

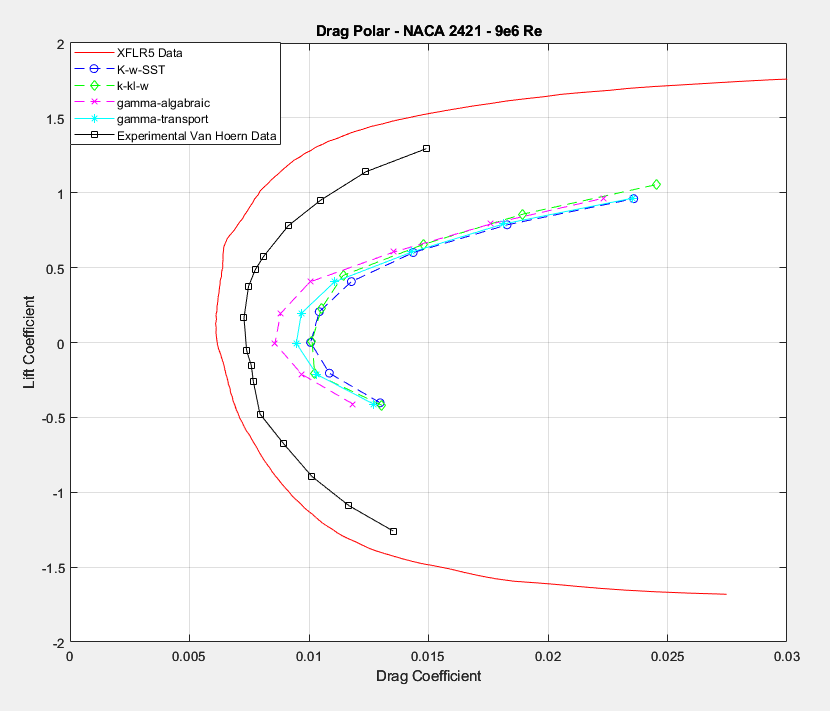
However, drag values are extremely sensitive to transition augment being used. In this case, the gamma algabraic seemed to provide the closest prediction for the drag values with gamma-transport being somewhat behind. Unfortunately, similar to the previous case, drag values at higher angles of attack are still massively higher than what they are, which is not acceptable. Xfoil continues to be a more reliable source for airfoil drag prediction at such reynolds numbers, especially given its massively lower computational cost and convenience.